Sejujurnya saya merasa betul-betul payah dalam membuat judul artikel (dan memang kenyataannya begitu). Sebenarnya pada artikel ini saya hanya membahas tentang pemahaman saya soal koordinat kurvalinear. Koordinat ini akan di pakai nantinya dalam melakukan simulasi cuaca yang berdomain bumi (bumi itu bulat #captainobvioushere). Karena Saya orangnya cepat lupa dan ingin mencari alasan untuk menulis pemahaman tentang topik ini di kepala saya cukup rumit jadi saya memutuskan untuk mendokumentasikannya saja.
Sebelum menulis artikel ini, sebenarnya saya berencana untuk melakukan simulasi prediksi suhu di wilayah Indonesia setelah cukup percaya diri di simulasi panas pada plat besi sebelumnya. Akan tetapi, di tengah jalan saya berhenti dan bertanya pada diri sendiri
Apa semudah ini? hanya dengan plot data pada grid dan jalankan simulasi?
Dan kemudian saya teringat fakta bahwa bumi itu bulat, tidak datar seperti plat besi sebelumnya (yeah, this is for you flat-eathers!). Dengan mengakui fakta ini, konsekuensinya beberapa persamaan yang melibatkan sumbu-sumbu pada koordinat kartesian harus di ubah sedikit.
Ok, apa itu koordinat kurvalinear? Koordinat kurvalinear adalah koordinat yang sumbu koordinatnya bukan garis lurus seperti kartesian melainkan garis kurva.
 |
| Koordinat kurvalinear (atas), kartesian (kiri), dan affine (kanan) untuk 2 dimensi. Terlihat Koordinat kurvalinear mirip seperti kartesian yang di dilipat dan dibengkokkan. |
Koordinat kurvalinear (u,v,w) bisa dibentuk dari 3 sumbu koordinat kartesian (x,y,z) begitu juga sebaliknya.
u = u(x,y,z)
v = v(x,y,z)
w = w(x,y,z)
x = x(u,v,w)
y = y(u,v,w)
z = z(u,v,w)
Sekarang anggap ada sebuah titik dR yang jika didefinisikan dalam koordinat kartesian akan seperti
dR = (dx,dy,dz)
Jika kita ingin mengetahui posisi dR tapi pada koordinat kurvalinear, maka seharusnya ini menjadi
Apa artinya itu? Kenapa tiba-tiba jadi begitu? Jadi, seperti yang sudah dikatakan sebelumnya kalau suatu titik di koordinat kartesian (x,y,z) itu bisa dicari juga titiknya di kurvalinear (u,v,w). Dan untuk mencarinya kita ambil diferensial parsial dari dR pada ketiga garis koordinat kurvalinear untuk mencari berapa besar "perubahan" yang terjadi kemudian dikalikan dengan du,dv, dan dw yang merupakan "pergeseran" yang di perlukan pada masing-masing sumbu koordinat kurvalinear. Jika setelah penjelasan ini masih sulit mencerna maksud dari persamaan di atas, maka disarankan untuk mempelajari terlebih dahulu tentang persamaan diferensial parsial...bukan, bukan tentang menghafalkan rumus lalu kerjakan soal dan dapat 100, bukan. Cukup pahami konsepnya saja (tapi yah, beberapa latihan itu perlu juga). Referensi yang bagus ada di khan academy dan betterexplained.
Kemudian anggap
dan unit length untuk melengkapi persamaan eu, ev, dan ew maka
Dan itulah persamaan umum untuk mencari nilai titik dari suatu koordinat ke koordinat kurvalinear. Kemudian, seperti yang sudah di katakan sebelumnya kalau perubahan sistem koordinat ini akan mengubah sedikit persamaan yang diterapkan pada domain tersebut. Contoh pada gradient tekanan
Ya, itu gradient yang berlaku pada koordinat kartesian. Lalu, bagaimana dengan gradient untuk koordinat kurvalinear dengan memperhitungkan gradient dari kartesian? yaitu dengan
Yang mana, ini mirip dengan hu, hv, dan hw (kali ini kita anggap (x,y,z) yang di turunkan terhadap (u,v,w) adalah hu, hv, dan hw juga secara berurutan) tadi, hanya saja kita tidak pakai R lagi karena "perubahan" di ukur per garis koordinat.
Nilai hu, hv, dan hw tergantung dengan koordinat kurvalinear yang digunakan. Tujuan kita mempelajari koordinat kurvalinear ini adalah untuk menurunkan persamaan yang dari koordinat kartesian ke koordinat bola (r, lintang, bujur) atau (r, θ, φ).
Karena koordinat bola melibatkan (r, θ, φ) maka 'h' yang terlibat dalam koordinat ini dinamakan hφ, hθ, dan hl untuk "mendatar", "vertikal", dan "ketebalan" dari pusat bumi. Terlihat di gambar bumi itu, jarak antar titik "mendatar" semakin pendek ketika mendekati kutub dan terpanjang ketika berada di equator. Sementara jarak antar titik "vertikal" selalu sama. Untuk jarak dari inti bumi sampai ke atmosfer terluar akan selalu kita anggap sama dengan jari-jari bumi karena
jari-jari bumi (a) >> ketebalan atmosfer
Dengan ini kita bisa menyimpulkan bahwa
Maka nilai dari hφ, hθ, dan hl adalah
Subtitusi ke persamaan gradient sebelumnya, maka (hu, hv, dan hw itu sama dengan hφ, hθ, dan hl)
Dan begitulah rumus gradient untuk bumi. Dan tidak hanya pada gradient. Selama rumus itu melibatkan penurunan terhadap sumbu koordinat atau semacamnya, maka penurunan itu harus di kalikan dengan suku 'h' yang telah di ketahui nilainya sesuai dengan garis koordinat apa yang diturunkannya itu (turunkan terhadap u, v, atau w).
Ya, cukup sekian catatan saya ini. Kali ini tidak ada buat program yang macam-macam. Nanti, jika ternyata ada suatu kesalahan pada artikel ini maka akan segera direvisi (saya sendiri masih kurang percaya diri dengan kemampuan matematikaku). Untuk itu, kritik dan saran silahkan tinggalkan di kolom komentar, sekian.
referensi:
http://sciencepole.com/geographic-coordinate-system/, di akses pada 7 Oktober 2016
https://en.wikipedia.org/wiki/Curvilinear_coordinates, di akses pada 6 Oktober 2016
https://en.wikipedia.org/wiki/Spherical_coordinate_system, di akses pada 6 Oktober 2016
http://www.jfoadi.me.uk/documents/lecture_mathphys2_05.pdf, di akses pada 5 Oktober 2016



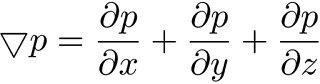




Komentar
Posting Komentar