 |
| Mau bagaimanapun kondisi awalnya, pada akhirnya panas akan terdistribusi merata |
Mari kita awali artikel ini dengan rant tidak jelas dari author :)) .
Keinginan terkuat adalah keinginan untuk bertahan hidup. Seluruh sistem dalam tubuh kita kecuali pikiran sadar (well, pikiran sadar yang membuat seseorang punya tendensi bunuh diri) berkonspirasi untuk melindungi diri kita (rasa sakit, alergi, rasa takut, rasa malu dll), membuat kita hidup nyaman walaupun itu berarti hidup dalam penjara pikiran. 'Ignorant is a bliss' is a fu*king true, gans. Keseluruhan sistem yang sangat mendorong kita berperilaku egois :) . Untungnya ini diimbangi dengan ketidakmampuan makhluk sombong ini untuk hidup sendiri, mau tidak mau makhluk egois ini harus bekerja sama membentuk simbiosis mutualisme, menciptakan win-win solution. Kebutuhan untuk menjadi egois mengharuskan kita untuk membantu dan berbagi dengan yang lain. Kalau sudah begini, apa gelar makhluk egois masih pantas di sandang oleh kita? Masih, kebaikan-kebaikan ini semua hanya status quo, ketika anda merugikan pihak yang lain...u and me end. Sinis sekali? lebih tepatnya realistis.
Ngomong-ngomong tidak lanjut deep learning lagi? Lanjut, tapi kita rehat sebentar dulu karena script softmaxku masih banyak errornya dengan rotasi materi lainnya, modelling. Ini materi yang cukup sederhana tapi saya lambat menyerapnya otak pas-pasan gan :)) .
Jadi, kita sudah pernah membahas sebelumnya juga tentang persamaan panas 1 dimensi, lantas apa yang spesial dari artikel ini? Kalau di artikel sebelumnya kita memakai skema eksplisit, sekarang kita akan memakai skema implisit.
Apa itu skema eksplisit dan implisit yang di maksud disini? Skema eksplisit ini adalah skema yang mana pada 1x penyelesaian, ada 1 variabel yang tak diketahui nilainya atau yang ingin dicari solusinya sedangkan pada skema implisit, variabel yang ingin dicari solusinya ada sebanyak jumlah grid spasialnya pada 1x penyelesaian.
Bagaimana cara mengetahui nilai variabel tersebut jika ada n variabel? Tentu saja kita butuh n persamaan linear yang tidak singular (jika singular, solusinya tidak unik dan solusi yang tidak unik itu tidak berguna dalam hal ini).
Cara tercepat untuk menyelesaikan sistem persamaan linear yang banyak adalah dengan membuat matriksnya dan menyelesaikannya dengan metode favorit anda (ada metode gauss, dekomposisi L U, gauss-jordan, dll).
Ax = b
dimana kita harus mencari solusi dari x. Pada sistem persamaan linear x dalam bentuk vektor yang isinya variabel-variabel yang dicari. A adalah koefisien dari variabel tersebut dan b adalah nilai yang diketahui.
Dengan dasar-dasar ini, selanjutnya kita akan mendiskritkan bentuk persamaan panas yang sedikit berbeda dengan artikel persamaan panas sebelumnya. Persamaan panas 1 dimensi bentuknya
dimana:
T = suhu
t = waktu
x = jarak sumbu x
k = konduktivitas thermal
Kemudian bentuk diskritnya
Perhatian, superscript disini bukan mengacu ke pangkat suatu bilangan tapi indexnya sama seperti subscriptnya. i mengacu ke index spasial (sumbu x) dan j index waktu sekarang (yang diketahui nilainya). Δx dan Δt mengacu ke jarak grid spasial dan waktu secara berturut-turut. Index j+1 mengacu ke keadaan yang akan di prediksi (variabel yang ingin di cari nilainya), mari kita atur ulang persamaan ini untuk memisahkan variabel yang diketahui nilainya dan tidak diketahui nilainya.
Dari sini kita bisa membentuk matriks Ax = b. Contoh penyelesaian kasus ini sudah saya buatkan scriptnya dan bisa di download di sini.
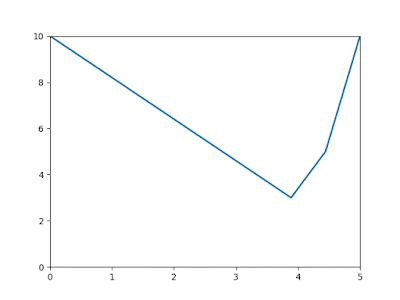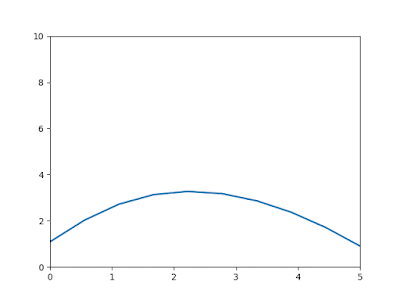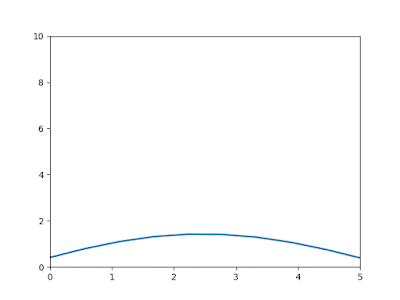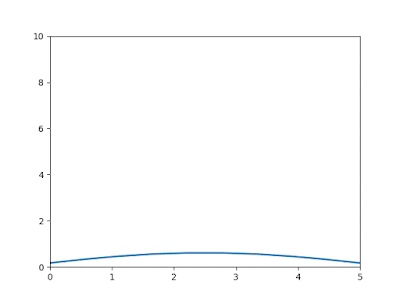 |
| Grafik perkembangan panas dari waktu ke waktu. Sumbu x untuk panjang benda dan sumbu y untuk besarnya suhu dalam celcius |
Salah satu kelebihan dari skema impilisit ini adalah kita tidak perlu memikirkan kondisi CFL yang mana ini merupakan batasan dalam mengambil time step atau spatial step pada skema eksplisit. Pada pemodelan fluida (Computational fluid dynamics) konon juga orang-orang lebih banyak memakai metode implisit ini karena lebih stabil dan errornya lebih kecil tapi belum ku uji coba sih, mungkin nanti kapan-kapan.
referensi:
http://www.dima.uniroma1.it/users/lsa_adn/MATERIALE/FDheat.pdf, diakses pada 1 Mei 2017
http://stackoverflow.com/questions/25140952/matplotlib-save-animation-in-gif-error, diakses pada 3 Mei 2017
http://stackoverflow.com/questions/16132798/python-animation-graph, diakses pada 3 Mei 2017



mohon disempurnakan. trims
BalasHapusnok"
Hapus