Penerapan Algoritma Genetik: Mencari Parameter Untuk Meminimalkan Fungsi Toytest

Apa itu fungsi Toytest? Fungsi toytest adalah suatu fungsi atau persamaan untuk mengetes performa algoritma yang ingin kita pakai, dalam hal ini algoritma optimasi. Ada banyak jenis fungsi toytest yang contoh-contoh bisa dilihat pada link ini.

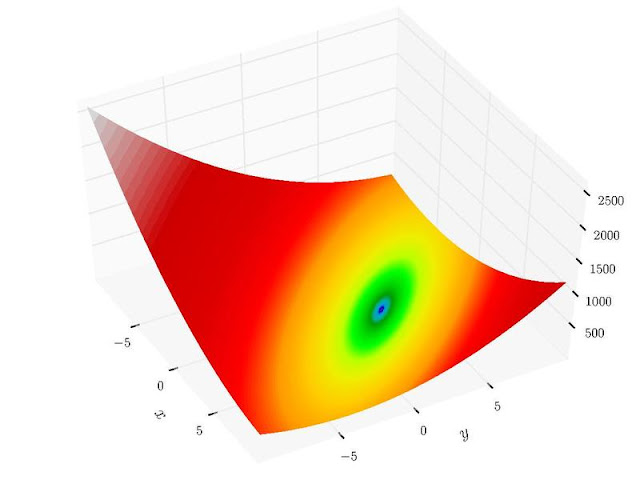
Dari daftar fungsi-fungsi pada link yang diberikan tersebut, kita memilih fungsi booth yang bentuknya adalah sebagai berikut

Di sini kita mencoba untuk mencari nilai x dan y agar keluaran fungsi ini mencapai nilai yang sekecil mungkin yaitu 0. Sehingga, fitness function kita adalah fungsi booth dan fitness yang paling baik adalah nilai fitness yang paling kecil. Nilai x dan y untuk mendapatkan keluaran 0 dari fungsi ini adalah 1 dan 3. Kita akan mencari nilai 1 dan 3 ini melalu algoritma genetik dengan "wilayah pencarian" atau search domain dari -10 dan 10.

Script yang kita gunakan untuk mencari nilai-nilai tersebut adalah dibawah ini

Jika tidak kelihatan, bisa klik di sini untuk mendownloadnya.

Algoritma dari script yang dibagikan di sini sama konsepnya seperti yang pernah dijelaskan pada pembahasan sebelumnya. Berikut uraiannya

1. Initialization

Di sini kita menginisialisasi solusi awal yang nilainya acak dengan search domain -10 sampai 10. Langkah ini cuma dilakukan sekali dan tidak masuk dalam iterasi sehingga iterasi dilakukan setelah langkah ini yang bisa dilihat pada full source code di atas yang menggunakan fungsi for.

2. Selection

Fase ini adalah fase yang masuk iterasi pertama kali bersama-sama dengan fase-fase selanjutnya, berbeda dengan fase initialization. Sama seperti pada penjelasan di postingan terdahulu, selection dilakukan berdasarkan nilai fitness function terbaik. Pada kasus ini, semakin kecil nilai dari fitness function maka solusi tersebut dianggap semakin baik. Oleh karena itu sebelum dilakukan selection, dilakukan terlebih dahulu pengukuran nilai fitness function untuk semua solusi yang ada sekarang. Lalu solusi-solusi itu disortir dari yang paling kecil sampai yang paling besar nilai fitness functionnya. Selection adalah fase yang sederhana dimana kita mengkeep beberapa jumlah solusi terbaik yang kita inginkan dan sisanya dibuang.

3. Crossover

Fase ini diawali dengan penentuan sepasang solusi yang akan melakukan crossover. Disini, sepasang solusi yang melakukan crossover akan melahirkan sepasang solusi baru juga. Kita tahu bahwa semakin baik kualitas pasangan solusi tersebut (dilihat dari nilai fitness fuction) maka kemungkinan besar solusi "anak"nya juga akan semakin baik. Oleh karena itu, solusi yang baik akan memiliki kemungkinan besar terpilih melakukan crossover dibanding dengan solusi yang kurang baik. Solusi yang kurang baik tetap diberi kesempatan untuk melakukan crossover karena mereka mempunyai kemungkinan memiliki "gen" yang baik untuk "masa depan" nanti atau bisa dibilang juga agar solusi final yang dihasilkan bukan berasal dari local optima, akan tetapi merupakan solusi sejati atau merupakan solusi dari global optima.

Penetuan mating pool atau kumpulan solusi-solusi yang akan melakukan crossover ditentukan pada baris 11-27 pada potongan script di atas. Bisa diliht di situ bahwa semakin baik ranking suatu solusi maka semakin besar kemungkinan solusi itu terpilih untuk masuk mating pool. Besarnya kemungkinan suatu solusi masuk mating pool pada script yang digunakan di sini adalah

Dimana survive adalah banyaknya solusi yang dikeep pada saat fase selection dan rank adalah ranking solusi yang ditinjau.

4.  Mutation

Solusi yang baru dilahirkan mempunyai kemungkinan kecil akan menyimpang sedikit dari induknya atau hasil crossover. Di sini kemungkinan penyimpangan itu terjadi adalah 20%. Ketika mutasi itu terjadi, pada solusi yang baru lahir tersebut untuk kasus ini, pada vektor solusi tersebut salah satu anggotanya nilainya akan menyimpang sedikit.

5. Pengaturan kembali populasi baru

Setelah fase 2, 3, dan 4 terlewati, selanjutnya adalah pengaturan populasi baru untuk menjalankan kembali fase 2, 3, dan 4 sampai nilai fitness function untuk solusi terbaik sudah memenuhi syarat yang diinginkan atau jumlah iterasi yang diinginkan sudah tercapai.

Contoh keluaran

Hasil running dari script yang dipakai di sini adalah sebagai berikut

Bisa dilihat bahwa iterasi yang dilakukan untuk setiap kali running bisa berbeda-beda (kita tahu bahwa script akan berhenti melakukan iterasi ketika nilai fitness function untuk solusi terbaik sudah dianggap memuaskan). Ini merupakan akibat dari algoritma genetik yang sifatnya acak cara kerjanya sama seperti neural network dan algoritma AI lainnya yang sering dibahas di sini. Bisa dilihat juga bahwa solusi terbaik yang dihasilkan tidak pas 1 dan 3 akan tetapi iterasinya tetap diakhiri. Untuk mendapatkan solusi yang lebih pas dengan nilai 1 dan 3 maka kriteria nilai fitness function yang dinginkan juga harus diperketat. Sekian.

referensi:
https://commons.wikimedia.org/wiki/File:Booth%27s_function.pdf, diakses pada 2 September 2018
https://en.wikipedia.org/wiki/Test_functions_for_optimization, diakses pada 2 September 2018